Normālais sadalījums

Normālais sadalījums jeb Gausa sadalījums ir viens no nepārtrauktiem varbūtību sadalījumiem. Piemēram, daudzu cilvēku kārtotā eksāmena atzīmes ir sadalītas normāli. Normālajam sadalījumam ir milzīga nozīme statistikā, tāpat tas tiek izmantots dabas zinātnēs un sociālajās zinātnēs, kur reālo gadījuma lielumu sadalījumi nav zināmi.

Normālais sadalījums

Blīvuma funkcija Sarkanā līkne abilst standarta normālajam sadalījumam.
Sadalījuma funkcija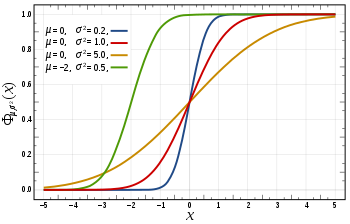
Apzīmējums	${\mathcal {N}}(\mu ,\sigma ^{2})$
Parametri	$\mu \in \mathbb {R}$ — matemātiskā cerība $\sigma ^{2}\in \mathbb {R} _{>0}$ — dispersija
Definēts	$x\in \mathbb {R}$
Blīvuma funkcija	${\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}$
Sadalījuma funkcija	$\Phi \left({\frac {x-\mu }{\sigma }}\right)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]$
Kvantiles	$\mu +\sigma {\sqrt {2}}\operatorname {erf} ^{-1}(2p-1)$
Vidējā vērtība	$\mu$
Mediāna	$\mu$
Moda	$\mu$
Dispersija	$\sigma ^{2}$
Vidējā absolūtā novirze	$\sigma {\sqrt {2/\pi }}$
Asimetrijas koeficients	$0$
Ekscesa koeficients	$0$
Entropija	${\frac {1}{2}}\log(2\pi e\sigma ^{2})$
Momentu ģenerējošā funkcija	$\exp(\mu t+\sigma ^{2}t^{2}/2)$
Raksturīgā funkcija	$\exp(i\mu t-\sigma ^{2}t^{2}/2)$
Fišera informācija	${\mathcal {I}}(\mu ,\sigma )={\begin{pmatrix}1/\sigma ^{2}&0\\0&2/\sigma ^{2}\end{pmatrix}}$ ${\mathcal {I}}(\mu ,\sigma ^{2})={\begin{pmatrix}1/\sigma ^{2}&0\\0&1/(2\sigma ^{4})\end{pmatrix}}$
Kullbaka-Leiblera diverģence	${1 \over 2}\left\{\left({\frac {\sigma _{0}}{\sigma _{1}}}\right)^{2}+{\frac {(\mu _{1}-\mu _{0})^{2}}{\sigma _{1}^{2}}}-1+\ln {\sigma _{1}^{2} \over \sigma _{0}^{2}}\right\}$
Sagaidāmais iztrūkums	$\mu -\sigma {\frac {{\frac {1}{\sqrt {2\pi }}}e^{\frac {-\left(q_{p}\left({\frac {X-\mu }{\sigma }}\right)\right)^{2}}{2}}}{1-p}}$

Normālais sadalījums ir ļoti noderīgs centrālo robežteorēmu dēļ, kas apgalvo, ka gadījuma lielumam sadalījums ir tuvs normālajam sadalījumam, ja tas ir vairāku citu savstarpēji neatkarīgu gadījuma lielumu summa. Normālais sadalījums dažkārt tiek saukts arī par zvanveida līkni, tomēr zvanveida formas sadalījums ir vairākiem sadalījumiem, piemēram, Košī un Stjūdenta.

Normālajam sadalījumam varbūtību blīvuma funkcija ir:

$f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}.$

Ja gadījuma lielums ir sadalīts normāli, tad to pieraksta kā ${\mathcal {N}}(\mu ,\,\sigma ^{2})$. Parametrs μ ir matemātiskā cerība, kas normālajam sadalījumam ir arī moda un mediāna. Parametrs blīvuma funkcijā σ ir standartnovirze, līdz ar to σ ² ir dispersija. Normālais sadalījums ir simetrisks attiecībā pret matemātisko cerību un ir nenegatīvs visā reālo skaitļu apgabalā.

Ja μ = 0 un σ = 1, tad sadalījums tiek saukts par standartizēto normālo sadalījumu.

Pilnīgi ideāls normālais sadalījums ir iespējams tikai teorētiski. Tādēļ parasti runā par atbilstību tam ar kādu noteiktu varbūtību, kas nozīmē pieļaujamās nobīdes no ideāla. To nosaka pēc asimetrijas un ekscesa koeficienta.

Ārējās saites

• Encyclopedia of Mathematics ieraksts (angliski)