Sagaidāmā vērtība

Sagaidāmā vērtība (arī matemātiskā cerība) varbūtību teorijā ir svērta vidējā vērtība. Ja katra gadījuma lieluma varbūtība notikt ir vienāda, sagaidāmā vērtība neatšķiras no vidējā aritmētiskā. Tā kā sagaidāmā vērtība ir netiešs lielums (aprēķināts, nevis izmērīts), tad bieži vien tieši šo vērtību nav iespējams iegūt (piemēram, vidējais cilvēks neeksistē). Ja gadījumu skaits ir galīgs, tad to aprēķina ar summu, bet bezgalīgā gadījumā (piemēram, reālu skaitļu intervālā) izmanto integrāli.

Piemērs sagaidāmai vērtībai - kolekcionēšana. Kolekcijai sastāvot no n elementiem, kāda ir sagaidāmā vērtība novēroto elementu skaitam, pirms ieraudzīta visa kolekcija?

Sagaidāmo vērtību gadījuma lielumam $X$ apzīmē ar $E(X)$, $E[X]$ vai $EX$.

Vēsture

Vēsturiski sagaidāmo vērtību pētīja punktu problēmā, kurā cenšas sadalīt spēles laimestu godīgi, ja tā tiek pārtraukta. Spēlei ir godīga veiksmes daba, kur abiem spēlētājiem ir vienādas izredzes uzvarēt katru partiju. Spēlētāji vienlīdz daudz piesola laimestam un piekrīt beigt spēli, kad kāds ir sasniedzis noteiktu skaitu uzvaru. Tad, pēkšņi, spēle tiek pārtraukta un nepieciešams sadalīt laimestu pareizi. Lai šo uzdevumu atrisinātu, nepieciešama gan skaitļošana, gan skaidrība par godīgumu. Problēmu pēc mūsdienu standartiem atrisināja 1654. gadā Blēzs Paskāls un Pjērs Fermā.

Lielo skaitļu likums

Lielo skaitļu likuma demonstrējums ar monētas varbūtībām

Ja no n neatkarīgiem eksperimentiem iegūst gadījuma lielumus x1, x2, ..., xn un izrēķina to vidējo aritmētisko ${\frac {x_{1}+x_{2}+...+x_{n}}{n}}$, tad, pieaugot n, rezultāts tieksies uz $E[X]$. Šis izpildās, ja gadījuma lieluma varbūtības nemainās, gadījumi ir neatkarīgi un $E[X]<\infty$.

Sagaidāmās vērtības gadījumi

Diskrētais gadījums

Ja gadījuma lielums X var pieņemt galīgu vērību skaitu {x1,..,xk}, kur katra lieluma vērtība ir {p1,...,pk}, tad sagaidāmo vērtību gadījuma lielumam X pieraksta kā:

$E[X]=x_{1}p_{1}+x_{2}p_{2}+...+x_{k}p_{k}$

Tā kā visu varbūtību summa ir 1, sagaidāmo vērtību var uzskatīt par svērto vidējo. Īpašajā gadījumā, ja visas varbūtības {p1, p2,...,pk} ir vienlīdz iespējamas, sagaidāmā vērtība sakrīt ar vidējo aritmētisko.

$\sum _{i=0}^{n}p_{i}=1$

Piemērs

Piemērs ar metamo kauliņu- gaidāmā vērtība vienam metienam ir 3,5, un, metienu skaitam tiecoties uz bezgalību, vidējā vērtība tiecas uz sagaidāmo vērtību.

• Apzīmēsim X kā iznākumu metamā kauliņa metienam. Iespējamās X vērtības ir 1, 2, 3, 4, 5, 6, kur katrai ir vienāda varbūtība uzkrist ${\frac {1}{6}}$. Sagaidāmā vērtība no X ir:$E[X]=1*{\frac {1}{6}}+2*{\frac {1}{6}}+3*{\frac {1}{6}}+4*{\frac {1}{6}}+5*{\frac {1}{6}}+6*{\frac {1}{6}}=3,5$

Saskaitāmi bezgalīgu gadījumu sagaidāmā vērtība

Neprecīzi var pierakstīt gaidāmo vērtību kā bezgalīgu summu:

$E[x]=\sum _{i=1}^{\infty }x_{i}*p_{i}$

Šis pieraksts ir neprecīzs, jo pastāv gadījumi, kad sagaidāmo vērtību šādi nevar definēt. Piemēram, ja absolūto xi vērtība tiecas uz bezgalību. Šādā gadījumā skaitļu secība nosaka rindas gala vērtību.

Piemēram, rinda 1 - 1 + 1/2 - 1/2 + 1/3 - 1/3 ... tiecas uz 0; bet rindas locekļu absolūtā summa (1 + 1 + 1/2 + 1/2 + 1/3 + 1/3...) tiecas uz bezgalību, tādēļ var pārkārtot rindu un iegūt citu robežvērtību. Piemēram, var saskaitīt pirmos divus pozitīvos locekļus un atņemt pirmo negatīvo: 1 + 1/2 - 1 + 1/3 + 1/4 - 1/2 + ... = ln 2

Nesaskaitāmi bezgalīgu gadījumu sagaidāmā vērtība

Sagaidāmo vērtību nesaskaitāmi bezgalīgā intervālā var pierakstīt kā integrāli:

$E[X]=\int _{\Omega }^{\,}X(r)*p(r)*dr$

Animācija, kā mainās$E(max(X))$ = ${\frac {n}{n+1}}$, mainoties $n$. Sagaidāmā vērtība ir laukums zem līknes

Piemērs

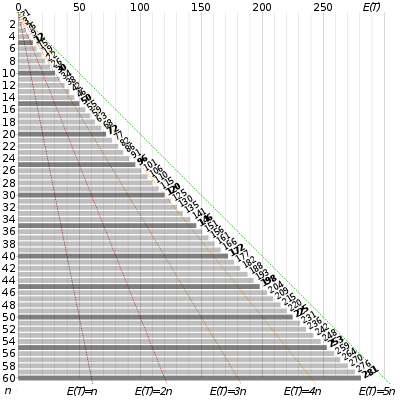
• Pieņemsim, ka katrs gadījuma lielums ir nejauši iegūts skaitlis no intervāla $[0,1]$. Ja notiek $n$ gadījuma lielumi, kāda ir gaidāmā vērtība lielākajam no gadījuma lielumiem?

Var veikt visu gadījumu pārbaudi ar kādu mainīgo $x$, kura vērtības nāk no dotā intervāla $[0,1]$. Lielākajam gadījuma lielumam būt mazākam par kādu $x$ nozīmē visiem skaitļiem būt mazākiem par $x$. Tā kā katrai gadījuma lieluma vērtībai ir vienāda varbūtība notikt, varbūtība katram atsevišķam gadījuma lielumam būt lielākam par $x$ ir $x$(šāda sakritība, jo intervāls $[0,1]$ sakrīt ar varbūtību intervālu). Šo varbūtību visiem gadījuma lielumiem var pierakstīt kā $P(x\geqslant max(X))=x^{n}$. Ja maksimālā vērtība ir lielāka par $x$, tad notiek tieši pretējais gadījums: $P(x<max(X))=1-x^{n}$. Tātad ir noformulēti lielumi, pēc kuriem noteikt sagaidāmo vērtību: mainīgais $x$, varbūtība $P(X)$ un vēl var izvēlēties gadījuma lielumu, kas būs 1, ja notiek $P(x<max(X))=1-x^{n}$ un 0, ja notiek pretējais $P(x\geqslant max(X))=x^{n}$. Tad iespējams aprēķināt sagaidāmo vērtību:

$\int (1-x^{n})dx=x-{\frac {x^{n+1}}{n+1}}+C$ , ievetojot mainīgā $x$ robežas 0,1, iegūst: $1-{\frac {1^{n+1}}{n+1}}+C-(0-{\frac {0^{n+1}}{n+1}}+C)=1-{\frac {1}{n+1}}={\frac {n}{n+1}}$

Jāpiebilst, ka tika izlaists $P(x\geqslant max(X))=x^{n}$ integrāļa pierakstā, jo tika pieņemts, ka šīs gadījuma lielums ir nulle (reizinājums ar nulli ir nulle).

Īpašības

Ja gadījuma lielumi X, Y rodas vienā procesā, tad izpildās: $E[X+Y]=E[X]+E[Y]$; $E[aX+b]=a*E[X]+b$

Ja $E[X]$ un $E[Y]$ nav atkarīgi viens no otra, tad $E[X*Y]=E[X]*E[Y]$