Kopu teorija

Kopu teorija ir matemātikas nozare, kas pēta kopas un to īpašības. Kaut gan kopas var sastāvēt no jebkādiem objektiem, kopu teorija parasti tiek lietota objektiem, kas ir saistīti ar matemātiku. Kopu teorijas valodu var izmantot gandrīz visu matemātisko objektu definīcijās.

Venna diagramma, kas attēlo divu kopu šķēlumu.

Modernos kopu teorijas pētījumus aizsāka Georgs Kantors un Rihards Dēdekinds ap 1870. gadu. Pēc paradoksu atklāšanas naivajā kopu teorijā, 20. gs. sākumā tika piedāvātas daudzas aksiomu sistēmas, no kurām labi pazīstamas ir Cermelo-Frenkela aksiomas un izvēles aksioma.

Pamatjēdzieni

Kopa

Kopa ir matemātikas pamatjēdziens, to nevar definēt ar citu jēdzienu palīdzību. Ar jēdzienu "kopa" matemātikā saprot vairākus priekšmetus vai objektus, kas apvienoti vienā veselā pēc kādas visiem tiem kopīgas pazīmes. Piemēram, Eiropas valstu kopa, pirmā kursa studentu kopa, visu naturālo skaitļu kopa.

Kopas elementi

Objekti, no kuriem veidotas kopas, var būt ne tikai materiāli priekšmeti, bet arī abstrakti jēdzieni, kā punkti, skaitļi, figūras u.t.t. Šos objektus, no kuriem viedojas kopa, sauc par kopas elementiem. Piemēram, naturālo skaitļu kopas $\mathbb {N}$ elementi ir 1, 2, 3, 4, ...

Kopas un tās elementu apzīmējumi

Kopas parasti apzīmē ar latīņu alfabēta lielajiem burtiem, bet kopu elementus - ar mazajiem burtiem. Attieksmi starp kopu un tās elementiem, ko izsaka ar vārdiem "būt elementam", "ietilpt kopā", apzīmē arī ar vārdu "piederēt".

Ja kāds objekts $x$ ir kopas $M$ elements, tad raksta $x\in M$ un lasa "$x$ pieder pie kopas $M$", "$x$ ir kopas $M$ elements".

Ja objekts $y$ nav kopas $M$ elements, tad raksta $y\not \in M$ jun lasa "$y$ nepieder pie kopas $M$", "$y$ nav kopas $M$ elements"

Kopu uzdošana matemātikā

Kopu uzskata par uzdotu, ja ir norādīta kāda pazīme, pēc kuras par jebkuru objektu var pateikt, vai tas pieder pie kopas vai nepieder. Visbiežāk kopas uzdod divos veidos:

1. sastāda pilnīgu un izsmeļošu kopas elementu sarakstu;
2. norāda īpašību, kas piemīt visiem aplūkojamās kopas elementiem un kas nepiemīt nevienam citam objektam.

Kopu pieraksts

Ja kopu uzdod ar pirmo veidu, tās elementus sarakstu ieslēdz figūriekavās. Piemēram, $\{a,b,c,d,e\}$; $\{$pavasaris, vasara, rudens, ziema$\}$.

Ja kopu uzdod ar otro veidu, tad figūriekavā vispirms raksta kopas elementu vispārīgo apzīmējumu, novelk vertikālu svītru un aiz tās raksta elementu raksturīgo īpašību.

Piemēram, $\{p|p$ ir pirmskaitlis$\}$, $\{b|b$ ir bērzi, kuru augstums pārsniedz 20 metrus$\}$.

Tukša kopa

Kopu, kura nesatur nevienu elementu sauc par tukšu kopu. Piemēram, $\{x|x$ ir naturāls skaitlis, kurš mazāks par 1$\}$. Tukšu kopu apzīmē ar simbolu $\varnothing$.

Galīgas kopas

Kopu sauc par galīgu, ja var saskaitīt tās elementus, vai arī, ja var pierādīt, ka elementu skaits kopā nepārsniedz iepriekš dotu naturālu skaitli.

Kopu $A=\{x,0,\gamma \}$ ir galīga, jo tajā ir trīs elementi.

Latvijas zaķu kopa. Protams, nevar precīzi pateikt, cik zaķu ir Latvijā, tomēr var droši apgalvot, ka zaķu skaits tajā nepārsniedz $10^{20}$.

Tukša kopa ir galīga, jo elementu skaits tajā ir 0.

Bezgalīgas kopas

Kopu, kurā elementu skaits ir lielāks nekā jebkurš iepriekš dots naturāls skaitlis $n$, sauc par bezgalīgu.

Taisnes punktu kopa, naturālu skaitļu kopa $\mathbb {N}$.

Eilera-Venna diagramma. Kopa $A$ iekļauj sevī visus kopas $B$ elementus.

Kopu grafiskā ilustrācija

Katru kopu var attēlot grafiski kā Eilera-Venna diagrammu, uzzīmējot slēgtu kontūru, pieņemot, ka dotās kopas elementus reprezentē iegūtās figūras punkti. Pašus punktus zīmējumā var arī neuzrādīt. Attēlā pa labi redzams, ka kopa $B$ ietilpst kopā $A$, kaut arī šajā zīmējumā tieši neredzam kopas $A$ un $B$ elementus un nezinām, kādas ir kopas $A$ un $B$.

Apakškopas

Kopu $B$ sauc par kopas $A$ apakškopu, ja katrs kopas $B$ elements ir arī kopas $A$ elements.

$B\subset A$, kopa $B$ ir kopas $A$ apakškopa, līdzvērtīgi $A\supset B$, kopa $A$ aptver kopu $B$. Attieksmes $B\subset A$ grafiskais attēlojums redzams zīmējumā.

Īstās un neīstās apakškopas

Matemātikā uzskata, ka tukša kopa $\varnothing$ ir katras kopas $M$ apakškopa. Kā arī pēc definīcijas kopa $M$ ir pati sev apakškopa. Pašu kopu $M$ un tukšo kopu $\varnothing$ sauc par kopas $M$ neīstām apakškopām.

Kopas $M$ jebkuru netukšu apakškopu, kas nav vienāda ar visu kopu $M$, sauc par kopas $M$ īstu apakškopu.

Vienādas kopas

Kopas sauc par vienādām, ja kopas $A$ un $B$ sastāv no vieniem un tiem pašiem elementiem. Kopas elementu secībai nav nozīmes.

Kopu vienādības pietiekamais un nepieciešamais nosacījums ir, ka kopas $A$ un $B$ ir vienādas tad un tikai tad, ja $A\subset B$ un arī $B\subset A$.

Attieksmju "$\subset$" un "$=$" transitīvā īpašība

Dažus spriedumus var vienkāršot izmantojot īpašības, ka

• ja $A\subset B$ un $B\subset C$, tad $A\subset C$
• ja $A=B$ un $B=C$, tad $A=C$

Darbības ar kopām

Ar kopām var veikt dažādas darbības, kuru rezultātā var iegūt jaunas kopas. Visu aplūkojamo objektu kopu sauc par universu jeb universālo kopu un apzīmē ar burtu $U$.

Kopu $A$ un $B$ šķēluma attēlojums ar Eilera-Venna diagrammu.

Kopu šķēlums

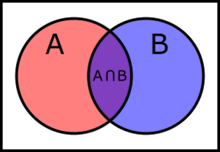
Par divu kopu $A$ un $B$ šķēlumu sauc kopu $C=$$A\cap B$, kura satur tos un tikai tos elementus, kuri pieder gan kopai $A$, gan kopai $B$.

$A\cap B=\{x|x\in A$ un $x\in B\}$

Īpašības:

1. Komutatīvā $A\cap B=B\cap A$;
2. Asociatīvā $(A\cap B)\cap C=A\cap (B\cap C)$;
3. $A\cap \varnothing =\varnothing$;
4. $A\cap U=A$;
5. Ja $B\subset A$, tad $A\cap B=B$.

Kopu $A$ un $B$ apvienojuma attēlojums, izmantojot Eilera-Venna diagrammu.

Kopu apvienojums

Par divu kopu $A$ un $B$ apvienojumu sauc kopu $C=A\cup B$, kas satur tos un tikai tos elementus, kas pieder vismaz vienai no abām kopām.

$A\cup B=\{x|x\in A$ vai $x\in B\}$

Kopu $A$ un $B$ starpības attēlojums, izmantojot Eilera-Venna diagrammu.

Īpašības:

1. Komutatīvā $A\cup B=B\cup A$;
2. Asociatīvā $(A\cup B)\cup C=A\cup (B\cup C)$;
3. Distrubutīvā īpašība:
   • Šķelšanās operācijai attiecībā pret apvienojuma operāciju $(A\cup B)\cap C=(A\cap C)\cup (B\cap C)$;
   • Apvienojuma operācijai attiecībā pret šķelšanās operāciju $(A\cap B)\cup C=(A\cup C)\cap (B\cup C)$;
4. $A\cup \varnothing =A$;
5. $A\cup U=U$
6. Ja $B\subset A$, tad $A\cup B=A$

Kopu starpība

Par divu kopu $A$ un $B$ starpību sauc kopu $C=A\backslash B$, kur satur tos un tikai tos kopas $A$ elementus, kas nepieder kopai $B$.

$A\ \backslash \ B=|\{x|x\in A$ un $x\notin B\}$

Kopas $B$ papildinājuma līdz kopai $A$, ja kopa $B\subset A$ attēlojums, izmantojot Eilera-Venna diagrammu.

Īpašības:

1. $A\ \backslash \ B=A\ \backslash \ (A\cap B)$;
2. $A\ \backslash \ (B\cap C)=(A\ \backslash \ B)\cup (A\ \backslash \ C)$;
3. $A\ \backslash \ (B\cup C)=(A\ \backslash \ B)\cap (A\ \backslash \ C)$;
4. $A\ \backslash \ A=\varnothing$;
5. $A\ \backslash \ \varnothing =A$;
6. Ja $B\subset C$, tad $B\ \backslash \ A=\varnothing$.

Kopas $A$ papildkopas attēlojums ar Eilera-Venna diagrammu.

Kopas papildinājums

Par kopas $B$ papildinājumu līdz kopai $A$ sauc kopu $B\ '_{A}$ , kas ir $A$ un $B$ starpība, ja kopa $B$ ir kopas $A$ apakškopa.

$B\ '_{A}=A\ \backslash \ B$, ja $B\subset A$

Par kopas $A$ papildkopu $A'$ sauc universālkopas $U$ visu to elementu kopu, kas nepieder kopai $A$.

$A\ '=A\ '_{U}=U\ \backslash \ A$

Īpašības:

1. $(A\cup B)\ '=A\ '\cap B\ '$;
2. $(A\cap B)\ '=A\ '\cup B\ '$;
3. $A\cap A\ '=\varnothing$;
4. $A\cup A\ '=U$.