Klasteru analīze

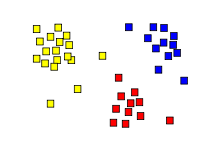
Klasteru analīzes galvenais mērķis ir sagrupēt novērojumus, balstoties uz to īpašībām, lai beigu objektu klasteri būtu ļoti homogēni klastera ietvaros, bet starp klasteriem heterogēni. Nosaukums klasteru analīzei cēlies no angļu vārda cluster — sakopojums, grupa. Termins klasteru analīze pirmo reizi lietots 1939. gadā, taču, ņemot vērā veiksmīga rezultāta iegūšanai veicamo loģisko un aritmētisko operāciju skaitu, tās plaša pielietošana kļuva iespējama tikai 1980. gados, attīstoties datortehnikai. No pārējām daudzdimensiju klasifikācijas metodēm tā atšķiras ar faktu, ka iepriekš nepastāv informācija par ģenerālās kopas sadalījumu, t.i., nav tā saucamo apmācības izlašu. Klasteru analīzi var uzskatīt kā aprakstošu un neteorētisku daudzdimensiju analīzes metodi, kas pārsvarā tiek izmantota kā palīglīdzeklis.

Skice - Klasteru analīzes sakopojums un pazīmju noteikšana

Analīzes soļi

Visiem pētījumiem, kas veikti izmantojot klasteru analīzi, ir raksturīgi sekojoši galvenie soļi:

1. datu atlase;
2. vairāku pazīmju noteikšana, pēc kurām tiks vērtēta pētāmā pazīme;
3. līdzības un attāluma mēra izvēle un aprēķināšana starp izlases objektiem;
4. klasteru analīzes izmantošana grupu izveidošanai (tā lai grupas būtu pēc iespējas homogēnākas);
5. iegūto rezultātu ticamības pārbaude.

Pielietojums

Klasteru analīzes metodoloģija ir plaši pielietojama medicīnā, arheoloģijā, psiholoģijā, kā arī mārketinga pētījumos. Šī metode ir vērtīgs datu analīzes rīks liela apjoma informācijas klasifikācijā tās tālākās apstrādāšanas nolūkos. Ar klasteru analīzi saprot nevis kādu noteiktu metodi, bet dažādu klasifikācijas algoritmu kopu, kas palīdz atrast atbildi uz kopējo pamatjautājumu — kā organizēt datus nozīmīgās struktūrās.

Klasteru pazīmes

Jebkuru klasteri var raksturot ar dažādām pazīmēm, kas sniedz labāku ieskatu klastera būtībā un paskaidro tā nozīmi. Jebkurš klasteris ir raksturojams ar šādiem pamata rādītājiem:

Blīvums

Šo rādītāju var izskaidrot, ja pētāmos datus attēlo kā punktus telpā. Klastera blīvums ļauj raksturot klasteri kā punktu sakopojumu datu telpā, blīvāku salīdzinājumā ar citiem telpas apgabaliem, kuros atrodas samērā maz punktu, vai arī nav vispār. Šis rādītājs sniedz acīmredzamu klastera jēdzienu, kaut arī viennozīmīga blīvuma mēra nav.

Dispersija

Dispersija raksturo datu izkliedi telpā attiecība pret klastera centru. Dispersija parāda, cik tuvu viens pie otra atrodas klastera punkti.

Izmērs

Ja ir iespējams identificēt klasteri, tad ir iespējams izmērīt arī tā rādiusu, taču tikai gadījumos, ja klasteris ir hipersfēra daudzdimensiju telpā, kuru apraksta objektu pazīmes.

Forma

Forma apraksta punktu izvietojumu telpā. Neskatoties uz to, ka parasti klasteri tiek attēloti kā hipersfēras jeb elipsoīdi, klasteriem mēdz būt arī citas formas.

Atdalīšanas pakāpe

Tā raksturo klasteru pārklāšanās pakāpi un to, cik tālu tie atrodas viens no otra. Saskaņā ar Everitta izvirzīto definīciju "klasteri ir noteiktās telpas nepārtraukti apgabali, ar salīdzinoši lielu punktu blīvumu, pie kam atdalīti viens no otra ar tādiem telpas apgabaliem, kur punktu blīvums ir salīdzinoši zems".

Nepilnības

Lai gan klasteru analīzes metode sniedz ļoti vienkāršu iespēju sagrupēt dotos datus, tādējādi ļaujot tālāk operēt ar homogēnām grupām, tomēr literatūrā tiek uzsvērtas arī šīs metodes nepilnības:

1. atkarībā no pielietojamās jomas, būtiski atšķiras arī dažādas klasteru analīzes metodes, līdz ar to viena metode nav universāla visām pētāmajām nozarēm;
2. dažādu klasteru metožu pielietošana var sniegt atšķirīgus rezultātus par vieniem un tiem pašiem datiem;
3. pārsvarā klasteru analīzes metodes ir vienkārši algoritmi, kuriem bieži ir nepietiekošs teorētiskais un statistiskais pamatojums.

Ārējās saites

• StatSoft mājaslapa Arhivēts 2015. gada 1. maijā, Wayback Machine vietnē.