Eksponenciālais sadalījums

Eksponenciālais sadalījums varbūtību teorijā ir nepātraukts varbūtību sadalījums. Šo sadalījumu izmanto, lai modelētu gaidīšanas laiku starp diviem notikumiem, kuri notiek nepārtraukti ar vienādu vidējo biežumu, un katrs nākamais notikums ir neatkarīgs no iepriekšējiem notikumiem. Šādā situācijā gaidīšanas laiki ir sadalīti eksponenciāli.

Eksponenciālais sadalījums

Blīvuma funkcija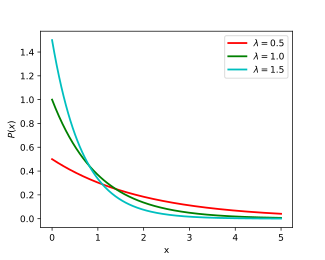
Sadalījuma funkcija
Parametri	$\lambda >0$
Definēts	$x\in [0,\infty )$
Blīvuma funkcija	$\lambda e^{-\lambda x}$
Sadalījuma funkcija	$1-e^{-\lambda x}$
Kvantiles	$-{\frac {\ln(1-p)}{\lambda }}$
Vidējā vērtība	${\frac {1}{\lambda }}$
Mediāna	${\frac {\ln 2}{\lambda }}$
Moda	$0$
Dispersija	${\frac {1}{\lambda ^{2}}}$
Asimetrijas koeficients	$2$
Ekscesa koeficients	$6$
Entropija	$1-\ln \lambda$
Momentu ģenerējošā funkcija	${\frac {\lambda }{\lambda -t}},{\text{ pie }}t<\lambda$
Raksturīgā funkcija	${\frac {\lambda }{\lambda -it}}$
Fišera informācija	${\frac {1}{\lambda ^{2}}}$
Kullbaka-Leiblera diverģence	$\ln {\frac {\lambda _{0}}{\lambda }}+{\frac {\lambda }{\lambda _{0}}}-1$
Sagaidāmais iztrūkums	${\frac {-\ln(1-p)+1}{\lambda }}$

Eksponenciālais sadalījums ir gamma sadalījuma speciālgadījums. To var uztvert kā nepātrauktu ģeometriskā sadalījuma analogu.

Eksponenciālā sadalījuma varbūtību blīvuma funkcija ir

$f(x)={\begin{cases}\lambda e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}$

Sadalījuma parametrs $\lambda$ ir pozitīvs skalas parametrs. Atbilstošā sadalījuma funkcija ir

$F(x)={\begin{cases}1-e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}$

Eksponenciāli sadalīta gadījuma lieluma $X$ matemātiskā cerība $\operatorname {E} [X]={\frac {1}{\lambda }}$, bet dispersija $\operatorname {D} [X]={\frac {1}{\lambda ^{2}}}$.

Eksponenciālo sadalījumu var izmantot, lai modelētu dažādus procesus, kas saistīti ar gaidīšanas laiku starp notikumiem, piemēram, laiku starp radioaktīvu daļiņu sabrukšanu, laiku starp diviem telefona zvaniem, laiku starp diviem veikala klientiem.

Skatīt arī

• Puasona sadalījums

Ārējās saites

• Vikikrātuvē par šo tēmu ir pieejami multivides faili. Skatīt: Eksponenciālais sadalījums.
• Encyclopedia of Mathematics ieraksts (angliski)
• Wolfram Mathworld ieraksts (angliski)