Ģeogrāfiskā koordinātu sistēma
Ģeogrāfiskā koordinātu sistēma (ĢKS) ir koordinātu sistēma, kur katru vietu uz zemeslodes raksturo ar trīs skaitļiem — koordinātām. Parasti tiek izmantota sfēriskā koordinātu sistēma. Ģeogrāfiskās koordinātas ir grādos izteikti attālumi no Zemes ekvatora (ģeogrāfiskais platums) un sākummeridiāna (ģeogrāfiskais garums).[1]

Zeme nav sfēra, bet gan neregulāras formas aptuvens elipsoīds, tāpēc, lai precīzi noteiktu atrašanās vietu, jāzina trīs koordinātas. Savukārt ja jānosaka tikai viena punkta atrašanās vietu uz Zemes virsmas, piemēram, pilsētas atrašanās vietu, var iztikt tikai ar divām koordinātām: viena nosaka tās ģeogrāfisko platumu, bet otra — ģeogrāfisko garumu.
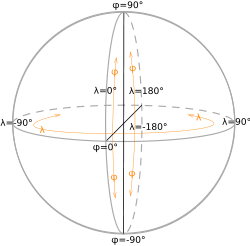
Attālumi starp paralēlēm un meridiāniem
labot šo sadaļuAttālumi starp paralēlēm
labot šo sadaļuAttālumu starp divām paralēlēm aprēķina pēc formulas:
| Platums | Z-D rādiuss |
Attālums par 1° izmaiņu |
1 minūtes izmaiņa | 1 sekundes izmaiņa |
|---|---|---|---|---|
| 0° | 6335,44 km | 110,574 km | 1842,9 m | 30,715 m |
| 15° | 6339,70 km | 110,649 km | 1844,15 m | 30,735 m |
| 30° | 6351,38 km | 110,852 km | 1847,53 m | 30,792 m |
| 45° | 6367,38 km | 111,132 km | 1852,2 m | 30,87 m |
| 60° | 6383,45 km | 111,412 km | 1857,01 m | 30,95 m |
| 75° | 6395,26 km | 111,618 km | 1860,3 m | 31,005 m |
| 90° | 6399,59 km | 111,694 km | 1861,566 m | 31,026 m |
Attālumi starp meridiāniem
labot šo sadaļuLīdzīgi aprēķina arī attālumu starp diviem meridiāniem:
| Platums | Grāds | Minūte | Sekunde | ±0,0001° |
|---|---|---|---|---|
| 60° | 55,65 km | 0,927km | 15,42 m | 5,56m |
| 57° | 60,527 km | 1,008km | 16,81 m | 6,05m |
| 45° | 78,7 km | 1,31km | 21,86 m | 7,87m |
| 30° | 96,39 km | 1,61km | 26,77 m | 9,63m |
| 0° | 111,3 km | 1,855km | 30,92 m | 11,13m |
| Platums | R-A rādiuss |
|---|---|
| 0° | 6378,14 km |
| 15° | 6379,57 km |
| 30° | 6383,48 km |
| 45° | 6388,84 km |
| 60° | 6394,21 km |
| 75° | 6398,15 km |
| 90° | 6399,59 km |
Atsauces
labot šo sadaļu- ↑ Anita Biseniece. Kontinentu ģeogrāfija 7. klasei. Zvaigzne ABC, 2007, 210. lpp.
Ārējās saites
labot šo sadaļu
| Šis ar ģeogrāfiju saistītais raksts ir nepilnīgs. Jūs varat dot savu ieguldījumu Vikipēdijā, papildinot to. |