Izliekums

Izliekums vai kurvatūra ir kāda no vairākām idejām ģeometrijā, kas intuitīvi apraksta cik lielā mērā līkne atšķiras no taisnes divās dimensijās vai kas apraksta virsmas atšķiršanos no plaknes trijās dimensijās.

Ģeometriski kāda punkta izliekumu var interpetēt ar riņķa līnijas palīdzību- izliekuma vērtība ir apgrieztā rādiusa vērtība $\kappa ={\frac {1}{R}}$, kur šī rādiusa riņķa līnija vislabāk apraksta funkcijas izliekumu šajā punktā.

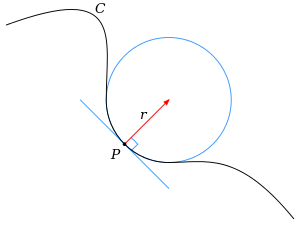
Līknēm kanoniskais piemērs ir riņķa līnija, kuras izliekums ir rādiusa apgrieztā vērtība $\kappa ={\frac {1}{R}}$. Mazākiem apļiem ir lielāks izliekums- tie vairāk atšķiras no taisnes nekā apļi ar lielāku rādiusu. Vispārīgāk, ja kāds punkts ir daļa no atvasināmas līknes, tad šī punkta izliekums ir vienāds ar tā riņķa izliekumu, kas vislabāk aptuveno izliekumu šajā punktā. Izliekums taisnei ir nulle. Izliekums parasti ir izteikts kā reāls skaitlis.

Priekš virsmām (vai, vispārīgāk, vēl augstāku dimensiju ķermeņiem), kuri atrodas Eiklīda telpā (3 vai vairāk dimensijās), izliekuma jēdziens ir vēl sarežģītāks, jo tas ir atkarīgs no virziena (kurus punktus uzskata par kaimiņiem). Šīs noved pie jēdzieniem maksimālais izliekums, minimālais izliekums un vidējais izliekums.

Līknes plaknē

Intuitīvi, izliekums apraksta cik ļoti līknes virziens mainās veicot nelielu distanci (piemēram, rad/m), tas ir mērs momentānai virziena maiņai. Citiem vārdiem, izliekums mēra cik ātri vienības tangensa vektors rotē kādā punktā P. Matemātiski var pierādīt, ka šī momentānā vienības tangensa vektora rotācija ir izliekums.

Izliekuma skaidrojums kā atvasinājums vienības tangensa vektoram visticamāk ir mazāk intuitīvs par oscilējošu riņķa līniju, kura izliekums sakrīt ar izliekumu kādā punktā. Tomēr vieglāk iegūt formulas izliekuma aprēķinam caur atvasinājumu tangensam.

Parabolas piemērs

Taisnes krāsa norāda vai funkcija ir ieliekta, izliekta vai nedz viena nedz otra. Zilā krāsa norāda ieliektus punktus, zaļā izliektus punktus.

Funkcijas otrais atvasinājums var iedot ideju kā grafika izliekums izskatīsies, bet izliekums ir atkarīgs arī no kā cita. Piemēram, vienkāršai parabolai $y=x^{2}$ otrais atvasinājums ir konstants visiem punktiem $y''=2$, taču izliekums nebūs konstants caur visu līkni, jo katrā parabolas punktā ir nepieciešams cita rādiusa riņķa līnija, lai tas labāk aprakstītu izliekumu.