Klucīšu kraušanas problēma

Klucīšu kraušanas problēma ir statikas uzdevums, kas apskata klucīšu kraušanu tā, lai to kaudzīte veidotu pārkari, vai arī karātos pāri, piemēram, galda malai. Tiek prasīts novietot $N$ identiskus, nestiepjamus, taisnstūrainus klucīšus tā, lai iegūtu maksimālu pārkari.

Pirmie deviņi klucīši viena klucīša platuma variantam

Cita uz citas sakrautu monētu kaudzīte — augšējā monēta vairs nemaz neatrodas virs pašas apakšējās monētas

Ir pieejams apkopots literatūras avots (Paterson et al. (2007)), kas ietver atsauces uz šo uzdevumu mehānikas mācību grāmatās no 19. gadsimta vidus.

Varianti

Ar vairākiem klucīšiem vienā "stāvā" iespējams iegūt lielāku rezultātu, nekā ņemot vērā viena klucīša platuma ierobežojumu

Viena klucīša platums

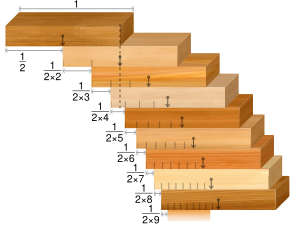
Viena klucīša platuma uzdevumā tikai viens klucītis var atrasties katrā "stāvā". Ideālajā gadījumā maksimālo pārkari var aprēķināt pēc formulas ${\frac {1}{2}}\cdot \sum _{i=1}^{N}{\frac {1}{i}}$. Tā kā šī apgriezto skaitļu rinda (harmoniskā rinda) diverģē, tad maksimālā pārkare tiecas uz bezgalību. Jāatzīst, nepieciešamais klucīšu skaits, lai pārkare palielinātos par vienu klucīša garumu, ļoti strauji pieaug. Mazākais klucīšu skaits, lai maksimālā pārkare ir vismaz $N$ klucīšu garumi, ir 4, 31, 227, 1674, 12367, 91380, ...

Vairāku klucīšu platums

Vairāki klucīši vienā "stāvā" var izmantot citus klucīšus kā pretsvarus. Pat ar trīs klucīšiem ir iespējams iegūt pārkari par veselu klucīti, turpretim viena klucīša platuma variants piedāvā 11/12 klucīša garumu kā pārkari.

Pierādījums viena klucīša platumam

Formulu maksimālajai pārkarei $N$ klucīšu gadījumā, kur katra klucīša garums ir $l$ un masa ir $m$ un tikai viens klucītis var atrasties katrā "stāvā", var pierādīt, ja apskata spēka momentus, kuri veidojas, pievienojot vienu klucīti klāt. Bāzes gadījumā ($n=1$), masas centrs atradīsies tieši uz galda malas un pārkare būs ${\frac {l}{2}}$ gara.

Ja klucīšu skaits ir $k$, var uzskatīt, ka virsējo $k-1$ klucīšu masas centrs atrodas tieši virs galda malas, tad tiek pievienots $k$-tais klucītis kaudzes apakšā ar pārkari $x$ un statiska līdzsvara gadījumā spēku momenti ir līdzsvarā:

$(k-1)mgx=({\frac {l}{2}}-x)mg\implies x={\frac {l}{2k}}$

No šī var secināt, ka katrs $k$-tais klucītis palielinās pārkari par $x_{k}={\frac {l}{2k}}$, jeb priekš $N$ klucīšiem maksimālā pārkare būs$x_{1}+x_{2}+x_{3}+...+x_{n}={\frac {l}{2\cdot 1}}+{\frac {l}{2\cdot 2}}+{\frac {l}{2\cdot 3}}+...+{\frac {l}{2\cdot n}}={\frac {l}{2}}\cdot \sum _{i=1}^{N}{\frac {1}{i}}$, kas arī bija jāpierāda.